Hash Table Implementation
Hash Tables are awesome. We know them as that super efficient data structure that can retrieve a value in constant time. But how is that actually possible?
Basics
Hash Tables are used to store key-value pairs. Each key must be unique, but values can repeat. To access a hash table value, you can usually do something like this:
ht = {"key1": "value1"}
print ht["key1"]
# => 'value1'But what does the underlying data structure look like?
Usually hash tables are represented as an array of elements since you can access an element in a collection in constant time as long as you know the index. This is the crux of how hash tables actually work.
A quick example of using an index to look up a value in an array
stuff = ["Thing1", "Thing2"]
stuff[1]
# => 'Thing2'When keys are created they are passed to a hash function which maps the item to a bucket (also called slots) in the array. A hash function usually does two things 1) creates a hash code - which is an integer 2) compresses the hash code to fit the current number of buckets - which becomes the index in the array where we want to store the value.
Creating a hash code can be as simple as just counting the number of characters in a key. Of course, this is far too simple to use for most purposes. More legit hashing methods include the folding method, mid-square method, and many more! However, for the purposes of this article we’ll just use the number of characters as the hash code. The hash code can then be compressed by dividing it by the number of buckets and taking the remainder to ensure the value actually correlates with an index in the array.
ht = [None, None, None]
new_key = "A key"
new_value = "A value"
hash_code = len(new_key)
# Compress hash code to fit in our hash table
hash_value = hash_code % len(ht)
# => 2
# Insert the value into our hash table
ht[2] = new_valueThen we can retrieve a value simply by using our hash function to find the bucket where our value should be and accessing that index in the array. But sadly, we’ve got a bit of a problem. What happens if two words are the same length and therefore have the same hash value? We’ve got a collision!
In our current implementation, the value would get overwritten. That’s no good. We’ve got to find a better way of dealing with this situation
Collisions
Ideally, we would have a perfect hashing function that always hashes a key to a unique index in the array. Unfortunately, with an arbitrary collection of keys and values, there’s no way to accomplish this. But we can find a way to deal with any resulting collisions. We’ll cover two popular ways of handling repeating keys.
Open Addressing
This method checks the slot indicated by the hashing function, realizes there’s already a value there, and simply places the value in the next available slot. By systematically visiting each slot one at a time, we are performing an open addressing technique called linear probing.
Let’s say we’re trying to add a key-value pair where the hash code (key length % number of bucket) matches a bucket that’s already full.

Linear probing would have us simply put the element in the next available bucket.
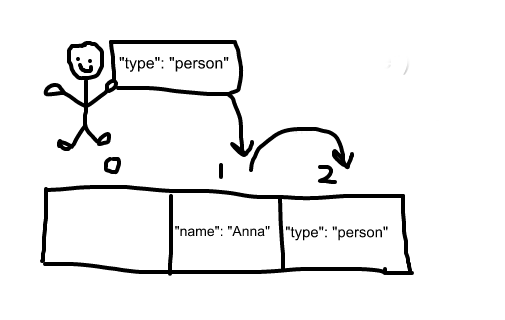
A common downside to linear probing is that items often become clustered in the table if there are many collisions at the same hash value.
One way to deal with clustering is to skip a designated number of buckets when searching for the next available slot after a collision (also known as rehashing) so items are spaced out. Quadratic probing and double hashing are a couple of common ways to avoid clustering.
Separate Chaining
Another popular method of dealing with collisions is to have each bucket in the hash table reference a linked list. This way you always know where your key-value pair will be stored, but you might have to iterate through the linked list in order to find it.
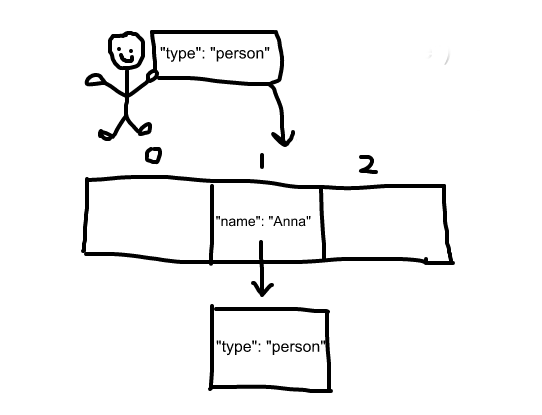
One thing to note, as more and more collisions occur at a specific index, the linked list can become long, which is annoying. This is a downside of this particular technique.
Scaling
A little bit about scaling. In our current implementation, there are only a set number of buckets in a hash table. This isn’t really what we want. What happens when they all get filled up? We would start getting some very long linked lists in each bucket. Instead, we really want it to be able to grow as more items are added.
If we keep track of the load factor of our hash (the number of buckets used / number of total buckets), we can then increase the capacity of our hash table whenever a certain percentage of the buckets becomes full. It’s important to note that all items already in the table will have to be re-added to the new larger table since the number of buckets have increased. Otherwise, we wouldn’t be able to find items we’ve added previously!
A Hash Table Implementation
I implemented a hash table in Python using separate chaining. You can find my code on Github. Would love any and all constructive feedback!